おさらい
前回の記事では、バトルサウンドで有名なメロディIC GSE3568 の同等品の M09 のサウンド構成を分析すべく、その出力をクロック単位でサンプリングしました。今回はそのサンプリングデータの分析を進め、同等のサウンドを ATtiny10 で再現する目途を立てます。

見た目で分析
サンプリングデータを分析するために、PHP でこんな分析補助スクリプトを作りました。使い捨てスクリプトなので根詰めて読んでいただく必要はありません。
<?php
/*
* キャプチャログを TSV化
*
* *.pulse.tsv パルス幅データ - パルスごとの幅(グラフ用)
* time, ON, OFF, freq
* *.freq.tsv 周波数時系列データ - 時刻ごとの周波数変化(グラフ用)
* time, freq
* *.tone.tsv トーン分析用データ - 同じ幅のパルスのカウント(分析用)
* time, ON, OFF, freq, cnt, l, t
* *.summary.tsv トーンサマリデータ - パルス幅毎のカウント(分析用)
* ON, OFF, freq, cnt
* *.raw 音声ファイル 8bit signed rawファイル
*/
// BIT0 CLOCK 128kHz
// BIT1 SOUND
// BIT2 LED
define('CLKRATE', 128000);
for($p = 1; $p < count($argv); $p++) {
decode($argv[$p]);
}
function decode($fn) {
$basenm = basename($fn, '.log');
$dat = file_get_contents($fn);
$trimpos = 0;
$wav = ''; // wavファイル出力バッファ
$tsv = [0]; // ランレングス 1長, 0長, 1長, 0長, ...
$ld = 1;
for($p = 0; $p < strlen($dat); $p++) {
$d = $dat[$p];
if ($d <= ' ') continue; // 行区切り等は無視
$d = (int)$d;
if ($d & 1) continue; // CLOCK 立ち上がりエッジは無視
$d = ($d & 2) ? 1 : 0;
if($trimpos == 0 && !$d) continue; // 左トリム
// wavファイル 8bit signed
$wav .= chr($d ? 0x7f : 0x80);
// ランレングスカウント
if($d == $ld) {
$tsv[count($tsv) - 1]++;
} else {
$tsv[] = 1;
$ld = $d;
}
// 最後の 1 の位置
if($d) $trimpos = strlen($wav);
}
// raw形式で wav出力
file_put_contents($basenm . '.raw', substr($wav, 0, $trimpos));
unset($wav);
// 最後の 1 と同じ幅の 0 とダミーレコードで終端
$p = count($tsv);
if ($p % 2 == 0) $p--;
$tsv[$p] = $tsv[$p - 1];
$tsv[] = 0;
$tsv[] = 0;
$r = CLKRATE;
// パルス幅 TSV 出力
$t = 0;
$buf = "time\tON\tOFF\tfreq\n";
for ($p = 0; $p < count($tsv); $p += 2) {
$on = $tsv[$p];
$off = $tsv[$p + 1];
$n = $on + $off;
$buf .= "${t}\t${on}\t${off}\t=${r}/${n}\n";
$t += $on + $off;
}
file_put_contents($basenm . '.pulse.tsv', $buf);
// 周波数時系列 TSV 出力
$t = 0;
$buf = "time\tfreq\n";
for ($p = 0; $p < count($tsv); $p += 2) {
$n = $tsv[$p] + $tsv[$p + 1];
for ($i = 0; $i < $n; $i++) {
$buf .= "${t}\t=${r}/${n}\n";
$t++;
}
}
file_put_contents($basenm . '.freq.tsv', $buf);
// トーン分析 TSV 出力とサマリ集計
$t = 0;
$buf = "time\tON\tOFF\tfreq\tcnt\tl\tt\n";
$lk = '';
$cnt = 0;
$summary = [];
for ($p = 0; $p < count($tsv); $p += 2) {
$on = $tsv[$p];
$off = $tsv[$p + 1];
$k = "${on}\t${off}";
@$summary[$k]++;
@$summary["${on}\t"]++;
@$summary["${off}\t"]++;
if ($k == $lk) {
$cnt++;
} else {
if ($cnt) {
$on = $tsv[$p - 2];
$off = $tsv[$p - 1];
$n = $on + $off;
$l = $n * $cnt;
$buf .= "${t}\t${on}\t${off}\t=${r}/${n}\t${cnt}\t${l}\t=${l}/${r}\n";
$t += $l;
}
$cnt = 1;
$lk = $k;
}
}
file_put_contents($basenm . '.tone.tsv', $buf);
// トーンサマリ出力
$buf = "ON\tOFF\tfreq\tcnt\n";
foreach ($summary as $k => $cnt) {
list($on, $off) = explode("\t", $k);
$n = $on + ($off ? $off : 0);
$buf .= "${k}\t=${r}/${n}\t${cnt}\n";
}
file_put_contents($basenm . '.sumarry.tsv', $buf);
}
これはサンプリングデータから各種 TSV を出力するもので、サウンドの周波数変化をグラフ化するためのデータだったり、サウンドの周波数とその長さの時系列(いわば楽譜のような)データだったりを出力するものです。スクリプトの中身の説明はしませんが、まずはサウンドとそのグラフを見ていただくことにします。
※音量注意!
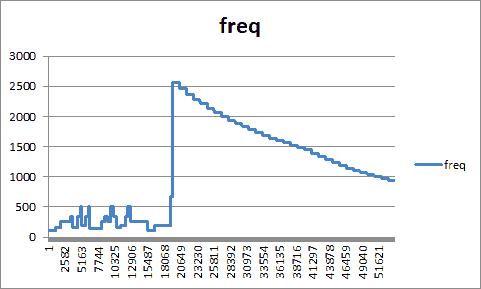
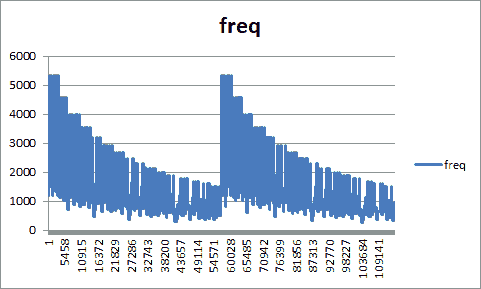
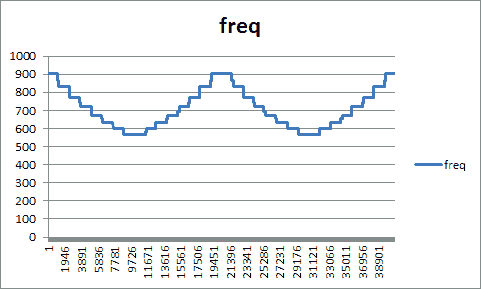
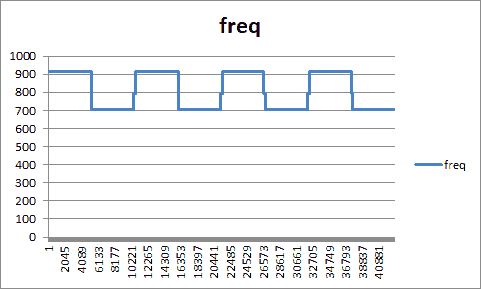
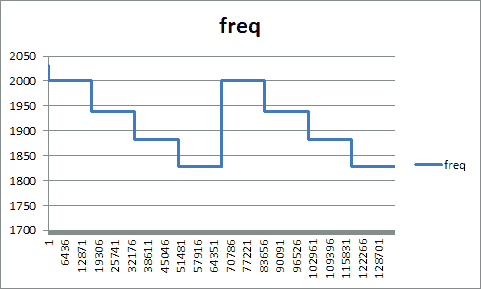
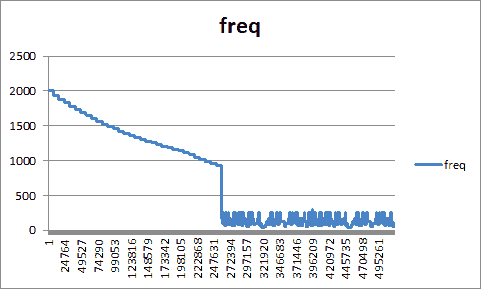
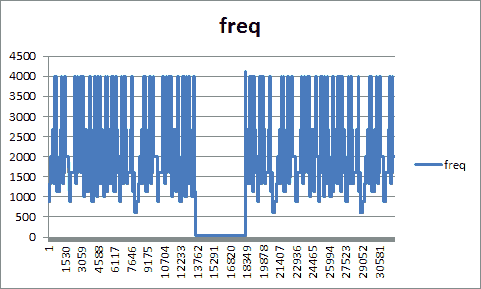
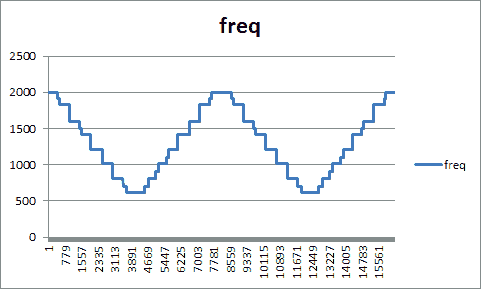
やはり視覚化してみると、聴いた感じと比べてもなるほどと思いますよね。周波数の範囲も把握できますし、ものによってはすぐ再現できそうだということも分かります。ちなみにこのグラフは Excel で描いてます。TSV で吐けばそのテキストをコピーして Excel に貼り付けてグラフ化したりできるのですから、とても便利です。
トーンの分析
サウンドはトーンとノイズで構成されていましたが、まずはトーンの分析です。これはもうグラフを見れば大体分かるというか、そんなに難しい話ではなさそうです。とりあえずこれを例に取って分析してみます。

分析補助スクリプトではグラフ表示のための TSV の他に、パルス幅(周波数)とその繰り返し回数としてサウンド構成をコンパクトにまとめた TSV(tone.tsv)も出力しています。このサウンドについてはこんな感じの内容になっています。これで全部です。小さいでしょう?
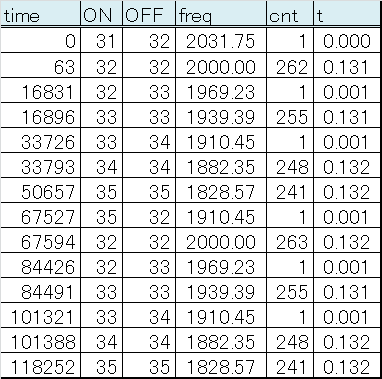
ON/OFF のカラムはパルスの ON と OFF の幅を 128kHz クロック数で示したもので、cnt はそのようなパルスが何周期繰り返されているかです。freq はパルスを周波数に換算したもの、t は繰り返しの長さを時間[秒] に換算したものです。周波数の切り替わり目にはその前後のパルス幅の中間のような感じになっている行もあって、そのような行は cnt が 1 のような小さな値になっているので判別できます。こういうのは前後の行に繰入るとスッキリしそうですね。これを見るに、2000Hz で始まり、1939Hz、1882Hz、1828Hz の 4種類の周波数が 131ms ほどで切り替わり、それを繰り返していることが分かります。このようにトーンの部分はほぼ機械的に答えを出せるので楽なものです。恐らく ATtiny10 での再現もそれほど苦労はしないでしょう。
参考に全サウンドについてのこのファイルを添付しておきます。
ノイズの分析
トーンの分析は簡単でしたが、ノイズはどうでしょうか。同じ調子のノイズが長めに続くこのサウンドを見てみます。

このサウンドは後半部分がノイズですが、どんな分析データになっているか抜粋してみます。
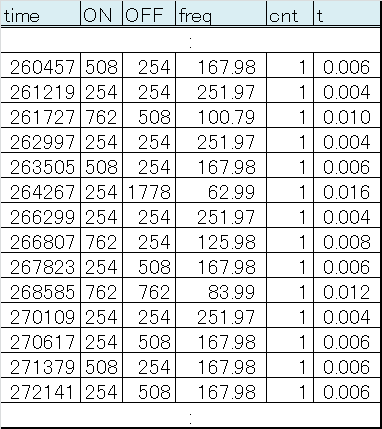
ノイズということで周期性に乏しく、パルス幅も様々で cnt も 1 の連続です。ただ、パルス幅が様々と言ってもなんとなく何種類かの数というか、何かの倍数のような、そんな雰囲気が感じられます。ぱっと見で 254 の倍数っぽいですね。ちょっと ON/OFF の値を 254 で割ってみます。
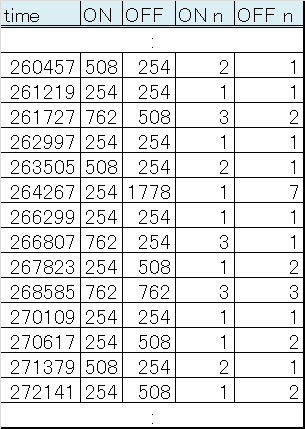
ビンゴです。254クロック幅を 1単位として、それが ON OFF それぞれランダムに何個かずつ並んでいるのですね。#6 のサウンドのノイズは 250Hz 程度が上限ですが、他のサウンドでは次の #2 のように 5.5kHz くらいまで伸びているのものがあります。ノイズの周波数によってこの 1単位のクロック数が 12クロック程度にまで縮まっているようです。


線形帰還シフトレジスタ(LFSR)
ノイズが一定幅を単位とするランダム長の ON OFF の並びで作られているということは分かりました。次はそのようなランダムな並びをどうやって作り出しているのかを突き止めなければなりません。ノーヒントでこの分析を行うのはやや無謀なのである程度アタリを付けて挑む必要がありますが、実は乱数の生成によく使われる「線形帰還シフトレジスタ(LFSR : Linear Feedback Shift Register)」というものがあります。

シフトレジスタというのは、その内容を右か左にずらす動作を行うことができる特定ビット幅のレジスタです。上図のシフトレジスタは 9bit幅で、一度に 1桁右にシフトします。そして LFSR では、シフトレジスタにタップというビットの取り出し位置を設けてあります。上図では bit0 と bit4 です。そしてタップの位置にあるビット値の XOR を取り、それをそのままかあるいは反転して(上図では反転)、シフト時の最上位ビットの新しい値として設定(フィードバック)します。タップはどこにでも何個でも選んでよいのですが、その選び方によってノイズの周期や性質が変わりますので、通常は周期が最も長くなるように工夫して選びます。ここで言う周期というのは、何回シフトするとレジスタの内容が元に戻るかということで、n bit の LFSR では 最大 (2^n) – 1 になります。9bit なら 511 です。
ちょっと 5bit の LFSR を動かして試してみましょう。
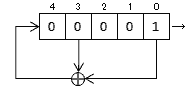
タップは bit0 と bit3、フィードバックの反転は無しです。現在の値は 00001 ですので、その出力は bit0 の 1 ということになります。そしてタップ位置の bit0 が 1 で bit3 は 0 ですから、その XOR は 1 です。一度シフトすると、この 1 が最上位ビット(bit4)の新しい値となります。といったことを繰り返したのが下の表です。
| STEP | レジスタ | STEP | レジスタ |
|---|---|---|---|
| 0 | 0 0 0 0 1 | 16 | 1 1 1 0 0 |
| 1 | 1 0 0 0 0 | 17 | 1 1 1 1 0 |
| 2 | 0 1 0 0 0 | 18 | 1 1 1 1 1 |
| 3 | 1 0 1 0 0 | 19 | 0 1 1 1 1 |
| 4 | 0 1 0 1 0 | 20 | 0 0 1 1 1 |
| 5 | 1 0 1 0 1 | 21 | 1 0 0 1 1 |
| 6 | 1 1 0 1 0 | 22 | 1 1 0 0 1 |
| 7 | 1 1 1 0 1 | 23 | 0 1 1 0 0 |
| 8 | 0 1 1 1 0 | 24 | 1 0 1 1 0 |
| 9 | 1 0 1 1 1 | 25 | 0 1 0 1 1 |
| 10 | 1 1 0 1 1 | 26 | 0 0 1 0 1 |
| 11 | 0 1 1 0 1 | 27 | 1 0 0 1 0 |
| 12 | 0 0 1 1 0 | 28 | 0 1 0 0 1 |
| 13 | 0 0 0 1 1 | 29 | 0 0 1 0 0 |
| 14 | 1 0 0 0 1 | 30 | 0 0 0 1 0 |
| 15 | 1 1 0 0 0 | 31 | 0 0 0 0 1 |
00000 以外の全ての値がまんべんなく現れ、STEP 31 で最初の値に戻っています。5bit の LFSR の最大周期は 31 になりますが、このタップの選び方は最大周期になるものでした。全ての値が出現するということはシフトレジスタの初期値は 00000 以外であればなんでもよく、最終的に同じ乱数のループになります。改めて上で求めた全ての STEP の bit0 を取っていくと 1 0 0 0 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 1 … となり、ノイズのようになかなか予測の難しい並びになっています。このように、LFSR は少ないリソースと非常に単純な方法で乱数的なビット列を得られる代表的なアルゴリズムの一つです。なので、メロディIC のような小さなハードウェアはノイズ生成に LFSR を使用しているのではないかと推定して分析してみます。
LFSR のパラメータを探す
LFSR のパラメータは、レジスタのビット長、タップ位置、フィードバックの際の反転・非反転です。なので、これを総当たりで探してみます。その前にノイズのビット列を抽出しておきます。

先ほどパルス幅を単位数に変換した上記のような表を作ることができましたが、これを順に読むと、ON が 2bit、OFF が 1bit ですので 110、次の行は ON が 1bit で OFF が 1bit で 10、同じように次が 11100 と繰り返して、それらを全て繋げて 11010111001011010000000… のようなビット列を得ます。そしてこのビット列を出力する LFSR のパラメータを探すと、こういうわけです。
総当たりは、レジスタのビット長からして不明ですからまずはビット長を 5~17bit 程度までの範囲で行うことにします。5bit の場合では、先ほど得たビット列の先頭 5bit(11010)をレジスタの初期値にします。ただし出力はレジスタの右側から出ていくので、レジスタに設定する時のビット順は逆順になり 01011 です。次に全てのタップ位置の組み合わせと、反転・非反転の組み合わせによって LFSR を動かし、お手本となるビット列とどの程度の長さ一致するかをパラメータ毎に調べていきます。それを行う PHP スクリプトはこんな感じです。
<?php
$s = '1101011100101101000000010111010011100010100110100110000111000001000101111100101001001000100111110100101000001010101011111101011010100001101000100011111100011000101101100001010001010111011011110011000111101000010010011001011110001000011110000000001111100001000001110100011001101111101101011000100101110000110000011001001110101011011100011100100101010001110110011101110111111110111101110011110110001101010100111100100001011001000110111010111101010010110000001001101101101001000000110110010101100110011111110011100';
// レジスタ初期値
$inireg = 0;
for ($b = 0; $b < 17; $b++) {
if ($s[$b] == 1) $inireg |= 1 << $b;
}
// レジスタ長検索
for($reglen = 5; $reglen <= 17; $reglen++) {
$all = ((1 << $reglen) - 1);
$msb = 1 << ($reglen - 1);
// タップ全検索
for ($fb = 0; $fb <= $all; $fb++) {
$reg = $inireg & $all;
$inv = $fb & 1; // 反転・非反転
$tap = $fb | 1; // タップ位置(bit0 は常に選択)
for ($b = $reglen; $b < strlen($s); $b++) {
$x = $inv ^ ($reg & $tap);
$x ^= $x >> 16;
$x ^= $x >> 8;
$x ^= $x >> 4;
$x ^= $x >> 2;
$x ^= $x >> 1;
$x &= 1;
if ($x != (int)$s[$b]) break;
$reg >>= 1;
if ($x) $reg |= $msb;
}
if ($b <= ($reglen * 2)) continue;
// 候補の表示
$taps = [];
for ($i = $reglen - 1; $i >= 0; $i--) {
if ($tap & (1 << $i)) $taps[] = $i;
}
if ($inv) $taps[] = 'inv';
echo sprintf("%dbit (%s) %d\n", $reglen, join(',', $taps), $b);
}
}実行結果はこんな感じです。
9bit (4,0,inv) 511
10bit (9,5,4,1,0) 511
11bit (9,6,4,2,0) 511
11bit (10,9,6,5,4,2,1,0,inv) 511
12bit (9,7,4,3,0) 511
12bit (10,9,7,5,4,3,1,0,inv) 511
12bit (11,9,7,6,4,3,2,0,inv) 511
12bit (11,10,9,7,6,5,4,3,2,1,0) 511
13bit (9,8,0) 511
:どうですか、お目当てのノイズと全く同じビット列を出す 9bit でタップ位置が bit0 と bit4、反転フィードバッグの LFSR が見つかりました!
ちなみに、実は冒頭で示した LFSR の図はこのパラメータに基づいたものでした。

検証
もろもろパラメータが分かったので、次のような PHP スクリプトでオーディオ出力を合成してみました。sgbase::noise 関数が LFSR の実装です。M09 のサンプリングレートは 128kHz でしたが、出力はよくある 44.1kHz にしてみました。冒頭の define で定義しているので、ある程度お好きなように変更いただけます。
<?php
define('ORGCLOCK', 128000);
define('OUTCLOCK', 44100);
class sound1 extends sgbase {
protected function gen()
{
// クロック数 19386
// 単位クロック数 128
$t = 19386 / ORGCLOCK;
$this->noise(128, $t);
// クロック数 34816
// ステップ数 32段
$t = 34816 / ORGCLOCK / 32;
// 20 steps
for ($w = 25; $w <= 44; $w++) {
$this->tone($w, $t);
}
// 12 steps
for ($w = 46; $w <= 68; $w += 2) {
$this->tone($w, $t);
}
}
}
class sound2 extends sgbase {
protected function gen()
{
// クロック数 57260
// 単位クロック数 12-42 2間隔 16段
$t = 57260 / ORGCLOCK / 16;
for ($i = 0; $i < 2; $i++) {
// 16 steps
for ($w = 12; $w <= 42; $w += 2) {
$this->noise($w, $t);
}
}
}
}
class sound3 extends sgbase {
protected function gen()
{
// クロック数 40859 (2往復合計)
// ステップ数 71-113 6間隔 8段 (片道1回)
$t = 40859 / ORGCLOCK / 4 / 8;
for ($i = 0; $i < 2; $i++) {
// 8 steps
for ($w = 71; $w <= 113; $w += 6) {
$this->tone($w, $t);
}
// 8 steps
for ($w = 113; $w >= 71; $w -= 6) {
$this->tone($w, $t);
}
}
}
}
class sound4 extends sgbase {
protected function gen()
{
// クロック数 37730 (4周期合計)
// ステップ数 70, 91 2段 (1周期分)
$t = 37730 / ORGCLOCK / 4 / 2;
for ($i = 0; $i < 4; $i++) {
$this->tone(70, $t);
$this->tone(91, $t);
}
}
}
class sound5 extends sgbase {
protected function gen()
{
// クロック数 135125 (2周期合計)
// ステップ数 32-35 4段 (1周期分)
$t = 135125 / ORGCLOCK / 2 / 4;
for ($i = 0; $i < 2; $i++) {
for ($w = 32; $w <= 35; $w++) {
$this->tone($w, $t);
}
}
}
}
class sound6 extends sgbase {
protected function gen()
{
// クロック数 260007
// ステップ数 32段
$t = 260007 / ORGCLOCK / 32;
// 25 steps
for ($w = 32; $w <= 56; $w++) {
$this->tone($w, $t);
}
// 7 steps
for ($w = 57; $w <= 69; $w += 2) {
$this->tone($w, $t);
}
// クロック数 260102
// 単位クロック数 254
$t = 260102 / ORGCLOCK;
$this->noise(254, $t);
}
}
class sound7 extends sgbase {
protected function gen()
{
// クロック数 13728
// 単位クロック数 16
// 間隔 4605
for ($i = 0; $i < 2; $i++) {
$t = 13728 / ORGCLOCK;
$this->noise(16, $t);
$t = 4605 / ORGCLOCK;
$this->wait($t);
}
}
}
class sound8 extends sgbase {
protected function gen()
{
// クロック数 16343 (2往復合計)
// ステップ数 32, 35, 40, 45, 53, 63, 79, 105 8段 (片道1回)
$t = 16343 / ORGCLOCK / 4 / 8;
$a = [32, 35, 40, 45, 53, 63, 79, 105];
for ($i = 0; $i < 2; $i++) {
foreach ($a as $w) {
$this->tone($w, $t);
}
foreach (array_reverse($a) as $w) {
$this->tone($w, $t);
}
}
}
}
(new sound1())->save('M09_clone1.raw');
(new sound2())->save('M09_clone2.raw');
(new sound3())->save('M09_clone3.raw');
(new sound4())->save('M09_clone4.raw');
(new sound5())->save('M09_clone5.raw');
(new sound6())->save('M09_clone6.raw');
(new sound7())->save('M09_clone7.raw');
(new sound8())->save('M09_clone8.raw');
// sound generator
abstract class sgbase
{
// サウンド生成ロジック
abstract protected function gen();
private $t;
private $wav;
private $nreg;
public function __construct()
{
$this->t = 0;
$this->wav = '';
$this->nreg = 0xeb;
}
// ファイル化
public function save($fn)
{
$this->gen();
file_put_contents($fn, $this->wav);
}
// トーン生成
protected function tone($w, $t)
{
$ow = $w * OUTCLOCK / ORGCLOCK;
$cnt = round($t * OUTCLOCK / (2 * $ow));
for ($i = 0; $i < $cnt; $i++) {
$this->out(1, $ow);
$this->out(0, $ow);
}
}
// ノイズ生成
protected function noise($w, $t)
{
$ow = $w * OUTCLOCK / ORGCLOCK;
$cnt = round($t * OUTCLOCK / $ow);
for ($i = 0; $i < $cnt; $i++) {
$nreg = $this->nreg;
$this->out($nreg & 1, $ow);
$par = $nreg & 0x011;
$nreg >>= 1;
if ($par == 0x00 || $par == 0x11) $nreg |= 0x100;
$this->nreg = $nreg;
}
}
// 無音
protected function wait($t)
{
$w = round($t * OUTCLOCK);
$this->out(0, $w);
}
// 波形データ生成
private function out($v, $w)
{
$t0 = (int)$this->t;
$this->t += $w;
$t1 = (int)$this->t;
$this->t -= $t1;
$this->wav .= str_repeat(chr($v ? 0x7f : 0x80), $t1 - $t0);
}
}
ちなみにオーディオファイルと言っても wavファイルではなく波形データだけが並んだバイナリファイルとして出力しています。このようなサンプリングデータを取り込めるソフトとして私は Windows の GoldWave というソフトを使っています。GoldWave はバイナリデータの羅列をサンプリングレート、サンプルのビット長と型(符号ありなしなど)、チャンネル数などを指定してオーディオとして読み込むことができて便利です。とりあえずパラメータの確認をすることが目的でしたので、ファイル化については気を使っていません。あしからず。
いずれにしましても、mp3 ファイル化しておきましたのでここで聞き比べていただけます。
いかがでしょう?なかなかの再現度じゃないですか?簡易的なサンプリングレート変換で時間軸の端数を切り捨ててる都合ヒョロヒョロした音が乗ってますが、確認には十分でしょう。とにかくアルゴリズムは合ってそうですね。
次回予告
トーンの分析およびノイズ生成アルゴリズムの特定もうまくいきました。やっぱりクロック同期で正確にサンプリングしておくとこの辺の手間が全然違います。ノイズビットパターンも、何度も聞き比べたりしなくともスクリプトで完全一致でパラメータ検索できてしまいます。ビットがズレてる可能性があるならこうはいきません。
これからもう少し精密なパラメータ化をした後、いよいよ ATtiny10 で実装です。サウンド出力は一定であるべきタイミングが揺らぐとすぐに変調がかったヒョロヒョロした音が出てしまうので、特にソフトウェアでリアルタイム生成しなければならないノイズをいかに正確なタイミングで出力できるかに苦労しそうな予感がします。この記事を書いている時点で ATtiny10 のコードとしてはただの 1行も書いていないので、私自身もまだその辺はっきり分かりません。案外あっさりできちゃうかもしれませんし。
といったところで、次回は完成したソースコードの公開とその解説になる予定です。それではまた。


